1. 简单的神经网络(Neural Network)
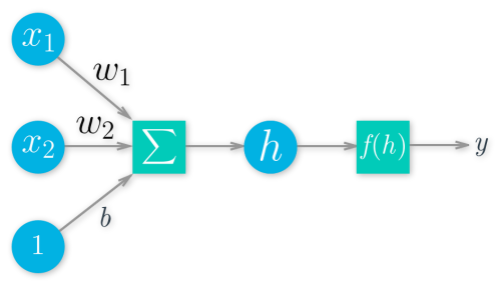
神经网络示意图,圆圈代表单元,方块是运算
这个架构使得神经网络可以实现,激活函数 f(h) 可以是任何函数,此例用
$$sigmoid(x)=\frac{1}{1+e^{-x}}$$
|
|
2. 重要的三个函数(Function)
- h(x) 即模型,也就是从输入特征预测输入的那个函数
$$h(x) = w_{1}x_{1} + w_{2}x_{2} + … + b , \text{其中w为权值,b为偏置项}$$
E(w) 目标函数 目标函数取最小(最大)值时所对应的参数值,就是模型的参数的最优值。很多时候我们只能获得目标函数的局部最小(最大)值,因此也只能得到模型参数的局部最优值。eg:
① 最小二乘式(一般用于回归类问题):
$$E(w) = \frac{1}{2}\sum\limits_{i=1}^n(y^{i}-\overline{y^{i}})^{2},其中,梯度 \Delta E(w) = -\sum\limits_{i=1}^n(y^{i}-\overline{y^{i}}) x^{i}$$② 交叉熵式(一般用于分类问题):
$$L(y,o)=-\frac{1}{N}\sum_{n\in{N}}{y_nlogo_n}$$f(x) 激活函数,常用的有sigmoid/relu/softmax
3. 随机梯度下降(Stochastic Gradient Descent,)
- 将预测值与实际值的误差$|y^{0}-y^{t}|$,组成的一个抛物线函数$|{y^{0}-y^{t}}|^2$,在抛物线里一直找梯度向下的方向,乘以步长$\eta$(也称作学习信率),不断地迭代,找出最小值。
- 梯度下降算法:
$$\mathrm{x}_{new}=\mathrm{x}_{old}-\eta\nabla{f(x)}\qquad(式3.1)$$
其中△为梯度算子,△f(x)是指f(x)的梯度,$\eta$步长
- 梯度下降算法可以写成:(△E(w)详细推导请看 △E(w)的推导 )
$$\mathrm{w}_{new}=\mathrm{w}_{old}-\eta\nabla{E(\mathrm{w})}\qquad(式3.2)$$
$$由于梯度: △E(w) = -\sum\limits_{i=1}^n(y^{i}-\overline{y^{i}}) x^{i} $$
- 因此,线性单元的参数修改规则最后是:
$$\mathrm{w}_{new}=\mathrm{w}_{old}+\eta\sum_{i=1}^{n}(y^{(i)}-\bar{y}^{(i)})\mathrm{x}^{(i)}\qquad(式3.3)$$
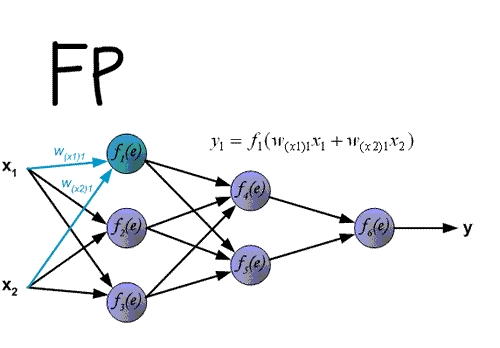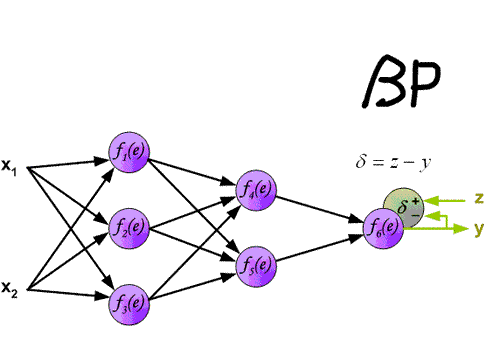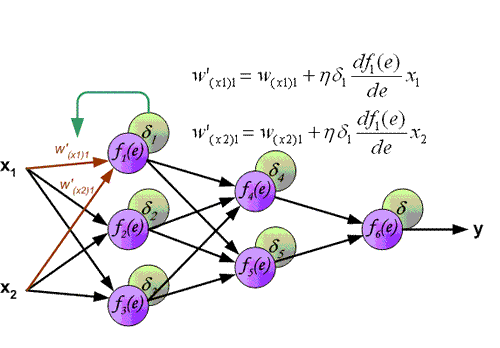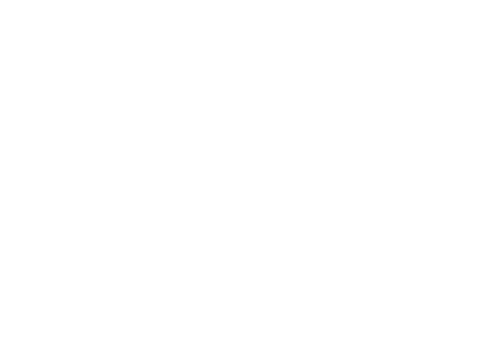
4. 前向传播(Forward Propagation)
- 在完成网络的每个层级时,计算每个神经元的输出。一个层级的所有输出变成下一层级神经元的输入。
5. 反向传播(Back Propagation)
在神经网络中使用权重将信号从输入层传播到输出层。使用权重将错误从输出层传播回网络,以便更新权重。
按照下面的方法计算出每个节点的误差项(error term) $\delta_i$
对于输出层节点i,
$$\delta_i=y_i(1-y_i)(t_i-y_i)\qquad(式5.1)$$对于隐藏层节点,
$$\delta_i=a_i(1-a_i)\sum_{k\in{outputs}}w_{ki}\delta_k\qquad(式5.2)$$梯度下降公式可表达为:
$$w_{ji}\gets w_{ji}+\eta\delta_jx_{ji}\qquad(式5.3)$$反向传播算法的详细推导请看 (反向传播算法的推导)
关于反向传播的推荐阅读(CS224n笔记5 反向传播与项目指导 - Hankcs )
-
6. 超参数的确定(Adjust Parameters)
选择迭代次数
也就是训练网络时从训练数据中抽样的批次数量。迭代次数越多,模型就与数据越拟合。但是,如果迭代次数太多,模型就无法很好地泛化到其他数据,这叫做过拟合。你需要选择一个使训练损失很低并且验证损失保持中等水平的数字。当你开始过拟合时,你会发现训练损失继续下降,但是验证损失开始上升。
选择学习速率$\eta$
速率可以调整权重更新幅度。如果速率太大,权重就会太大,导致网络无法与数据相拟合。建议从 0.1 开始。如果网络在与数据拟合时遇到问题,尝试降低学习速率。注意,学习速率越低,权重更新的步长就越小,神经网络收敛的时间就越长。
选择隐藏节点数量
隐藏节点越多,模型的预测结果就越准确。尝试不同的隐藏节点的数量,看看对性能有何影响。你可以查看损失字典,寻找网络性能指标。如果隐藏单元的数量太少,那么模型就没有足够的空间进行学习,如果太多,则学习方向就有太多的选择。选择隐藏单元数量的技巧在于找到合适的平衡点。
- 调整根据经验,下面有几个经验公式:
\begin{align}
&m=\sqrt{n+l}+\alpha\\
&m=log_2n\\
&m=\sqrt{nl}\\
&m:隐藏层节点数\\
&n:输入层节点数\\
&l:输出层节点数\\
&\alpha:1到10之间的常数
\end{align}