1. Bellman方程(Bellman Equation)
贝尔曼方程(Bellman Equation)也被称作动态规划方程(Dynamic Programming Equation),由理查·贝尔曼(Richard Bellman)发现。贝尔曼方程是动态规划(Dynamic Programming)这些数学最佳化方法能够达到最佳化的必要条件。
贝尔曼方程表明当前状态的值函数与下个状态的值函数的关系。
见下图,第一层的空心圆代表当前状态(state),向下连接的实心圆代表当前状态可以执行两个动作,第三层代表执行完某个动作后可能到达的状态 s’。
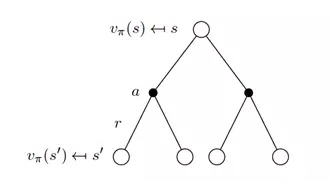
根据上图得出状态价值函数公式:
\begin{align}
v_{\pi}(s)=E[U_t|S_t=s]=\sum_{a\in A}\pi(a|s)\,\left( R_s^a+\gamma \sum_{s’\in S}P^a_{ss’}v_{\pi}(s’)\right)
\end{align}
其中:
\begin{align}
P_{ss’}^a = P(S_{t+1}=s’|S_t=s, A_t=a)
\end{align}
上式中策略π是指给定状态 s 的情况下,动作 a 的概率分布,即:
\begin{align}
\pi(a|s)=P(a|s)
\end{align}
将概率和转换为期望,上式等价于:
\begin{align}
v_{\pi}(s) = E_{\pi}[R_s^a + \gamma v_{\pi}(S_{t+1}|S_t=s]
\end{align}
同理,我们可以得到动作价值函数的公式如下:
\begin{align}
q_{\pi}(s,a)=E_{\pi}[R_{t+1}+\gamma q_{\pi}(S_{t+1},A_{t+1})|S_t=s,A_t=a]
\end{align}
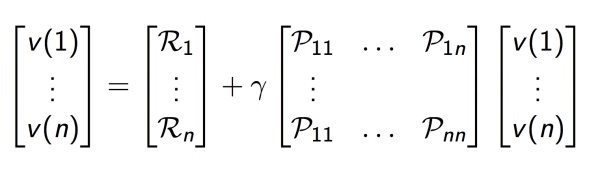
如上图,Bellman 方程也可以表达成矩阵形式:
\begin{align}
v=R+\gamma Pv
\end{align}
可直接求出:
\begin{align}
v=(I-\gamma P)^{-1}R
\end{align}
其复杂度为:
\begin{align}
O(n^3)
\end{align}
一般可通过动态规划、时间差分法与蒙特卡洛估计求解。
● 通过解 Bellman 最优性方程找一个最优策略需要以下条件:
动态模型已知
拥有足够的计算空间和时间
系统满足 Markov 特性
2. 状态价值函数和动作价值函数的关系
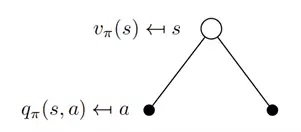
\begin{align}
v_{\pi}(s) = \sum_{a \in A} \pi(a|s)q_{\pi}(s,a) = E[q_{\pi}(s,a)|S_t=s]
\end{align}
\begin{align}
q_{\pi}(s,a) = R_s^a + \gamma \sum_{s’\in S}P_{ss’}^a \sum_{a’ \in A}\pi(a’|s’)q_{\pi}(s’,a’) = R_s^a+\gamma \sum_{s’ \in S} P_{ss’}^a v_{\pi}(s’)
\end{align}
3. 最优方程
\begin{align}
v_(s)= \max_aq_(s,a)= \max_a\left( R_s^a + \gamma\sum_{s’\in S}P_{ss’}^a v_(s’) \right) \\
q_(s,a)= R_s^a+\gamma \sum_{s’\in S}P_{ss’}^av_(s’) = R_s^a + \gamma \sum_{s’ \in S}P_{ss’}^a\max_{a’}q_(s’,a’)
\end{align}
● v 描述了处于一个状态的长期最优化价值,即在这个状态下考虑到所有可能发生的后续动作,并且都挑选最优的动作来执行的情况下,这个状态的价值
● q 描述了处于一个状态并执行某个动作后所带来的长期最优价值,即在这个状态下执行某一特定动作后,考虑再之后所有可能处于的状态并且在这些状态下总是选取最优动作来执行所带来的长期价值
4. 最优策略
关于收敛性:(对策略定义一个偏序)
$\pi \ge \pi’ \,\mbox{if}\; v_{\pi}(s)\ge v_{\pi’}(s),\forall s$
定理:
对于任意 MDP:
总是存在一个最优策略π*,它比其它任何策略都要好,或者至少一样好
所有最优决策都达到最优值函数, $v_{\pi_}(s)=v_(s)$
所有最优决策都达到最优行动值函数,$q_{\pi_}(s,a)=q_(s,a)$
最优策略可从最优状态价值函数或者最优动作价值函数得出:
\begin{align}
\pi_(a|s) =
\begin{cases}
1, & \mbox{if } a = \arg\max_{a \in A} q_(s,a)\\
0, & otherwise
\end{cases}
\end{align}