Bellman最优解策略 - 动态规划法(Dynamic Programming Methods)
动态规划是一种通过把复杂问题划分为子问题,并对自问题进行求解,最后把子问题的解结合起来解决原问题的方法。
「动态」是指问题由一系列的状态组成,而且状态能一步步地改变。
「规划」即优化每一个子问题。因为MDP 的 Markov 特性,即某一时刻的子问题仅仅取决于上一时刻的子问题的 action,并且 Bellman 方程可以递归地切分子问题。
1. 策略估计(Policy Evaluation)
对于任意的策略π,我们如何计算其状态值函数Vπ(s)?这个问题被称作策略估计。
● 基于当前的 Policy 计算出每个状态的 Value function
● 同步更新:每次迭代更新所有的状态的 v
\begin{align}
V_{k+1}(s)=\sum_{a\in A}\pi(a|s)\left( R_s^a+\gamma\sum_{s’\in S}P_{ss’}^av_k(s’)\right)
\end{align}
● 矩阵形式:
\begin{align}
\mathbf{v^{k+1}=R^{\pi}+\gamma P^{\pi}v^k}
\end{align}
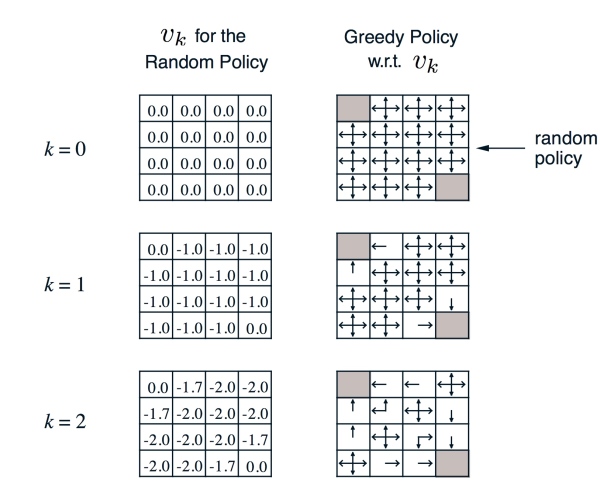
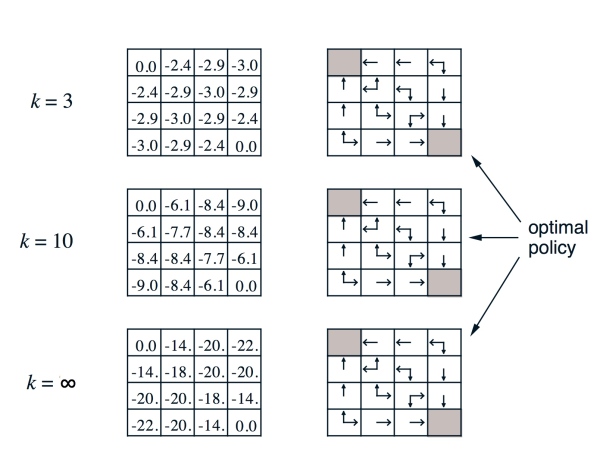
● 左边是第 k 次迭代每个 state 上状态价值函数的值,右边是通过贪心(greedy)算法找到策略
● 计算实例:
\begin{align}
k=2, -1.7 \approx -1.75 = 0.25(-1+0) + 0.25(-1-1) + 0.25(-1-1) + 0.25(-1-1)
\end{align}
\begin{align}
k=3, -2.9 \approx -2.925 = -0.25(-1-2) + 0.25(-1-2) + 0.25(-1-2) + 0.25(-1-1.7)
\end{align}
2. 策略改进(Policy Improvement)
● 基于当前的状态价值函数(value function),用贪心算法找到最优策略
$\pi’(s)=\arg\max_{a\in A} q_{\pi}(s,a)$
● Vπ会一直迭代到收敛,具体证明如图:
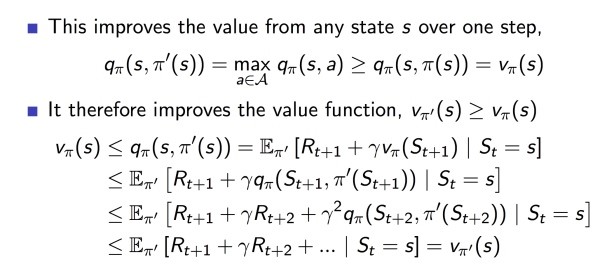
事实上在大多数情况下 Policy evaluation 不必要非常逼近最优值,这时我们通常引入 \epsilon-convergence 函数来控制迭代停止。
很多情况下价值函数还未完全收敛,Policy 就已经最优,所以在每次迭代之后都可以更新策略(Policy),当策略无变化时停止迭代。
3. 策略迭代(Policy Iteration)
策略迭代算法就是策略估计和策略改进两节内容的组合。假设有一个策略π,那么可以用policy evaluation获得它的值函数Vπ(s),然后根据policy improvement得到更好的策略π’,接着再计算Vπ’(s),再获得更好的策略π’’。
4. 价值迭代(Value Iteration)
最优化原理:当且仅当状态 s 达到任意能到达的状态 s‘ 时,价值函数 v 能在当前策略(policy)下达到最优,即$v_{\pi}(s’) = v_(s’)$,与此同时,状态 s 也能基于当前策略达到最优,即$v_{\pi}(s) = v_(s)$
状态转移公式为:
$v_{k+1}(s) = \max_{a\in A}(R^a_s+\gamma\sum_{s’ \in S}P^a_{ss’}v_k(s’))$
矩阵形式为:$\mathbf{v_{k+1}} =\max_{a \in A} \mathbf{R^a_s} +\gamma\mathbf{P^av_k})$
下面是一个实例,求每个格子到终点的最短距离,走一步的 reward 是 -1:
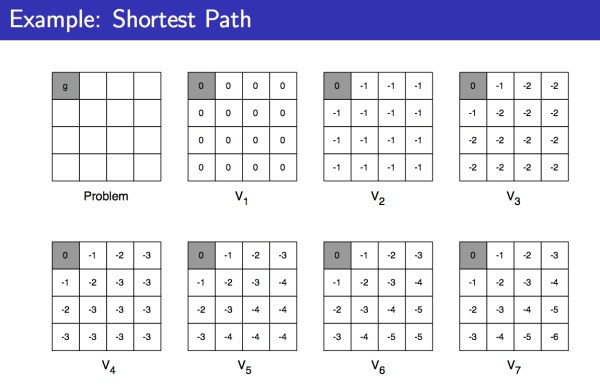
同步动态规划算法小结
MDP 的问题主要分两类:
① Prediction 问题
输入:MDP (S,A,P,R,y)和策略(policy)π
输出:状态价值函数 Vπ
② Control 问题
输入:MDP (S,A,P,R.y)
输出:最优状态价值函数V*和最优策略π
● 策略估计(Policy Evaluation)解决的是 Prediction 问题,使用了贝尔曼期望方程(Bellman Expectation Equation)
● 策略改进(Policy Improvement)解决的是 Control 问题,实质是在迭代策略评估之后加一个选择 Policy 的过程,使用的是贝尔曼期望方程和贪心算法
● 策略迭代(Policy Iteration)解决的是 Control 问题,实质是在迭代策略评估之后加一个选择 Policy 的过程,使用的是贝尔曼期望方程和贪心算法
● 价值迭代(Value Iteration) 解决的是 Control 问题,它并没有直接计算策略(Policy),而是在得到最优的基于策略的价值函数之后推导出最优的 Policy,使用的是贝尔曼最优化方程(Bellman Optimality Equation)